hyen4110.tistory.com/6?category=934053
[통계] 03 표본분포(Sampling distribution)
표본분포 기초 이론에 들어가기에 앞서, 어떻게, 왜 표본분포를 통해 모집단의 특성(모수)를 추정할 수 있는지 살펴보겠습니다. 1. [Why] 표본조사는 왜 하는가? -> '전수조사의 대안, 표본조사' 어
hyen4110.tistory.com
지금까지는 모집단이 1개였을 때에는, 모집단으로부터 표본분포를 구한 후
우리가 수집한 표본i가 표본분포 상에 존재하는 값임을 이용하여
표본분포의 평균과 표본i의 평균의 차이가 얼마나 유의미한지 계산하였습니다. (위의 이전 글 참고)

그렇다면, 두 집단을 비교하는 문제에서는 무엇을 비교해야 할까요?
-> '두 모집단의 평균이 얼마나 차이나는지 비교해야 한다'
-> '두 모집단의 평균의 차이가 0인지 비교한다'
-> '두 모집단의 평균의 차이가 이루는 분포'를 얻은 후, 0값과 비교!
-> 각 모집단의 표본평균분포의 차이(x̅₁ - x̅₂)에 대한 분포와 0값을 비교!
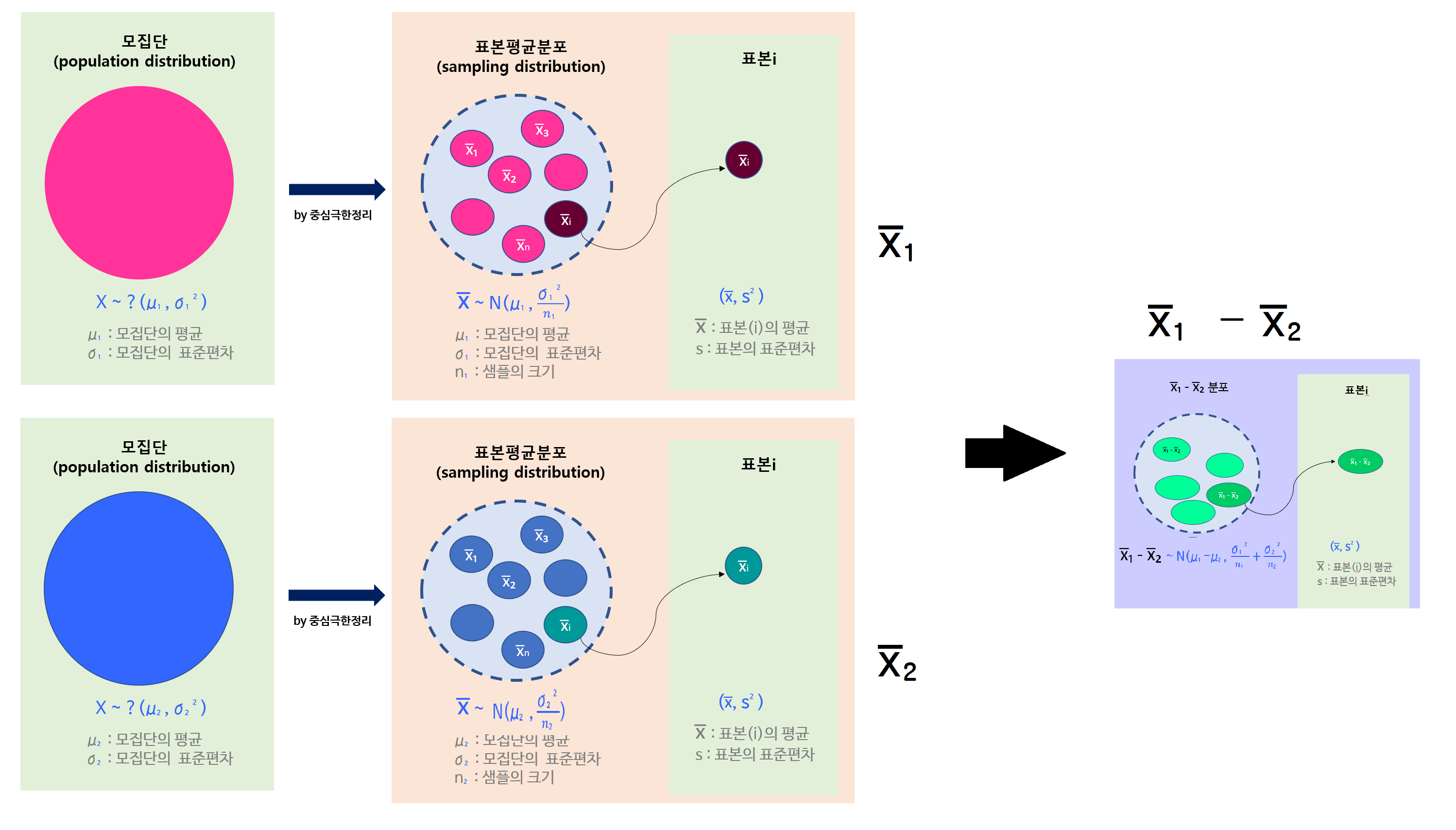
| 모집단1 | 모집단2 | 두 표본평균분포의 차이 | |
| 모집단 |  |
 |
|
| 표본평균분포 |  |
 |
 |
두 표본분포의차이 (x̅₁ - x̅₂)에 대한 평균과 분산값의 계산과정은 아래와 같습니다

위에 대한 개념은 아래 이미지를 참고하세요!

- 이 후로는 모집단이 1개인 표본조사에서의 추정과 동일합니다!
- 각 모집단의 표본평균분포의 차이(x̅₁ - x̅₂)의 분포를 찾았고
그 분포 위에 존재하는 값(표본조사를 통해서 각 모집단으로부터 얻은 평균의 차이)도 얻었습니다.
이제 해야할것은 z값 또는 t값을 구하여 검정을 실시하는 것입니다.


I. 독립표본 T검정 (Dependent Sample T-test)
- 두 표본이 각 모집단으로부터 독립적으로 추출되었다는 가정
- 한 표본이 다른 표본의 값에 영향을 주지 않는다.

1-1. 등분산(Equal Variance)의 경우
1) 모분산이 알려진 경우

2) 모분산을 모르는 경우

- Sp²는 모분산 대신에 사용되는 표본분산이다.
- Sp²는 S₁²와 S₂²의 평균으로 통합분산(pooled variance)이라고도 한다.

1.2 이분산(Unequal variance)의 경우
1) 이분산임을 어떻게 판단하지? -> 등분산 검정
: 두 집단의 분산이 같다는 가설에 대한 검증으로, 등분산 검정을 통해 등분산/이분산 여부를 알 수있다.
: F-test를 통해 검증한다.

1) df1, df2 두 자유도를 가지고 Fc.v를 구한다
2) 두 집단의 표본의 분산의 비율로 F값을 구하여 Fc.v와 비교한다
2) 이분산인 경우

: 이분산의 경우, 통합분산 Sp를 쓰지 않고 S₁와 S₂로 따로 계산한다.
: T-test에서 자유도는 등분산과 다르다! (매우매우 복잡!)

'Statistics' 카테고리의 다른 글
| [통계] 상관관계(Correlation Coefficient) (6) | 2021.05.23 |
|---|---|
| [통계] 카이제곱 검정(Chi-squre test) (1) | 2021.04.27 |
| [통계] 04 가설검정_1, 2종 오류와 유의수준 (0) | 2021.04.19 |
| [통계] 03 표본분포(Sampling distribution) (0) | 2021.04.19 |
| [통계] 02 정규분포(Normal distribution) (0) | 2021.04.19 |




댓글