1. 상관관계(Correlation Coefficient)
1.1 상관관계란?
- [의미] 상관관계는 두 변수 간의 직선관계를 나타냅니다. 상관관계가 있다는 것은 인과관계가 있다는것이 아닙니다. 상관관계가 높다고해서 두 변수에서 하나의 변수가 다른 변수의 원인을 설명할수는 없습니다. 이유는 알 수 없지만, 상관관계가 높을 뿐이죠.
- [부호] 상관관계 값이 0에 가까울수록 직선관계가 없으며, -1에 가까울수록 강한 음의관계, +1에 가까울수록 강한 양의 관계를 가집니다.
- [지표] 상관관계를 나타내는 지표를 상관계수라고 합니다. 대표적인 상관계수로는 피어슨 상관계수, 스피어만 상관계수가 있습니다.
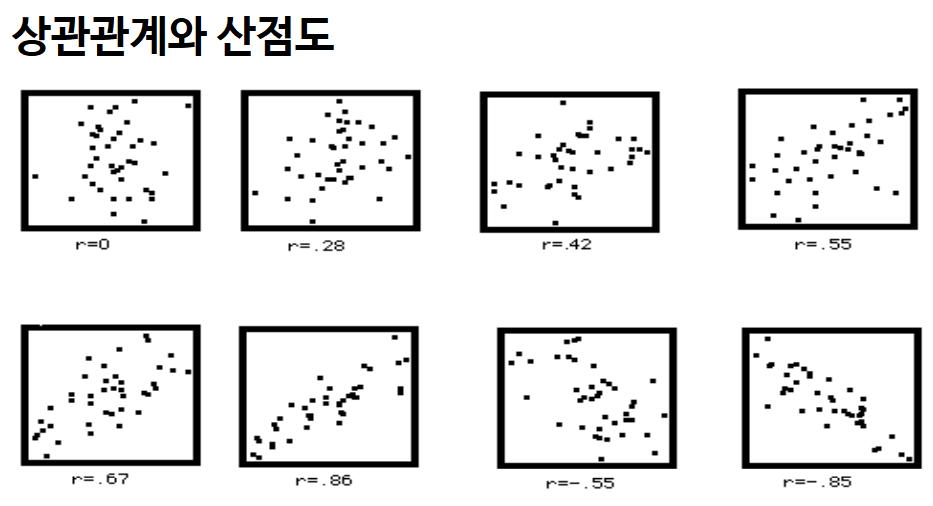
- 상관관계를 분석하는데 있어서 가장 기본적이고 직관적인 방법은 산점도를 살펴보는 것입니다. 산점도에서 분포가 직선에 가까울수록 상관관계가 높다고 할 수 있습니다.
2. 상관관계의 지표
2.1 공분산(Covariance)
- [의미] 공분산(covariance)은 2개의 확률변수의 선형 관계를 나타내는 값(위키피디아) 이라고 합니다. 위에서 본 상관관계의 정의와 거의 일치하죠. 하지만 사실상 공분산은 상관계수로 쓰이지 않습니다. 그 이유는 변수의 단위에 영향을 많이 받기 때문입니다. 아래에서 다시 한 번 설명하도록 하겠습니다.
- [부호] 공분산의 값은, 두 변수가 선형관계가 없는 경우 0을 가지며, 두 변수가 비례하는 경우 양수의 값, 반비례의 경우 음수의 값을 갖습니다.
| 분산(Variance) | 공분산(Coveriance) |
| 변수 1개의 분포 형태 | 변수 2개의 분포 형태 |
| 표본의 편차제곱의 평균 | X의 편차와 Y 편차를 곱한 것의 평균 |
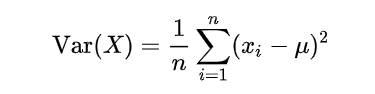 |
 |
- 빠른 이해를 위해서 아주 간단한 예제를 하나 보고 가겠습니다.
: 아래는 데이터의 개수가 3인 변수 X,Y가 있습니다. 이 변수의 공분산과 상관계수를 구하는 과정을 아래 그림으로 살펴보겠습니다.


2.2 피어슨 상관계수(Pearson Correlation Coefficient ,PCC)
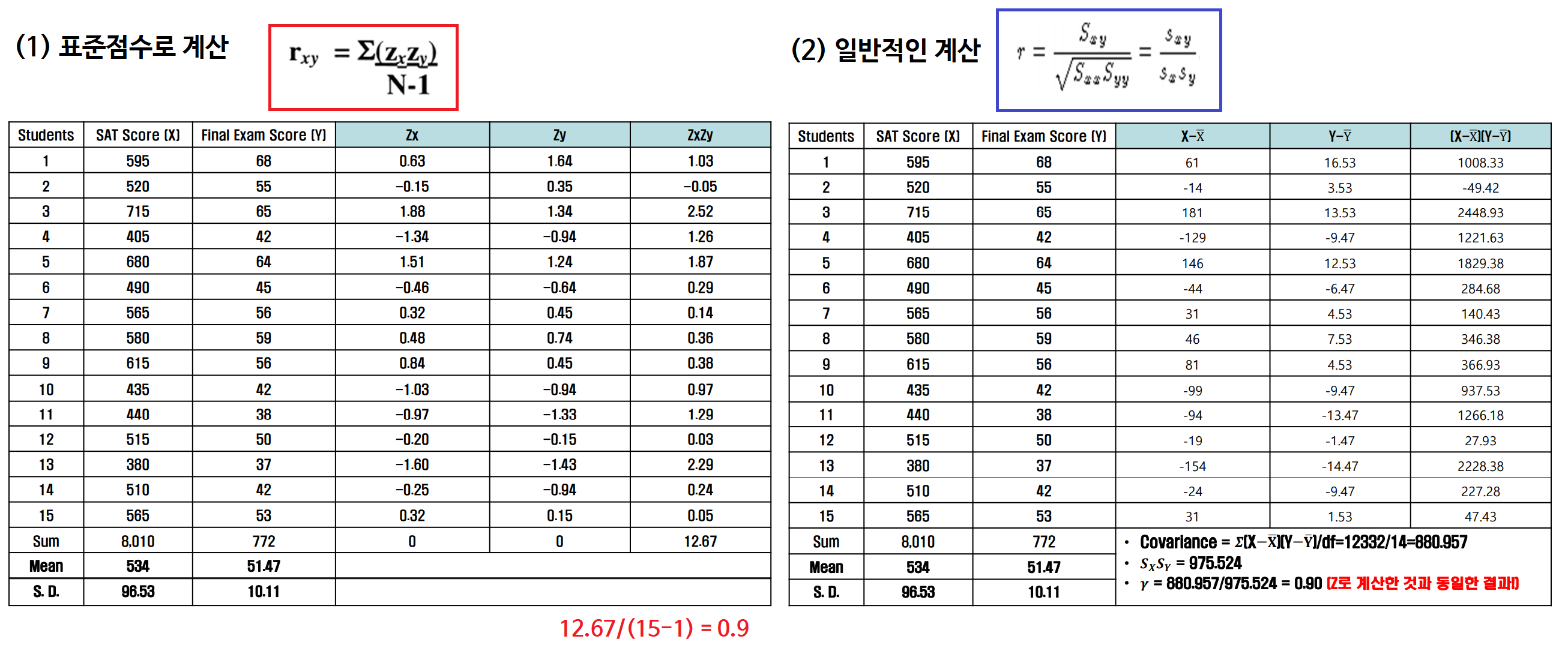
- 위에서 구한 상관계수가 바로 피어슨 상관계수입니다.

- 피어스 상관계수는 표준점수(Z)값을 통해서 구하는 방법도 있는데요, 아래 이미지와 같습니다.
: 표준점수로 계산할 시 (N-1)로 나누어준다는 것을 기억하면 되겠습니다!
2.3 스피어만 상관계수(Spearman Correlation)
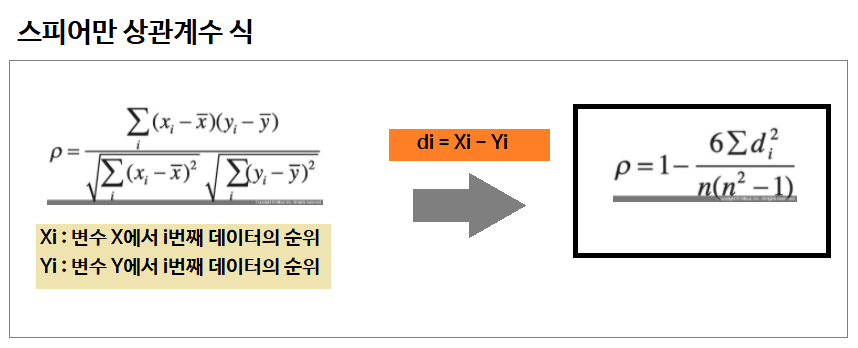
- 스피어먼 상관 계수는 "순위가 매겨진 변수 간의 피어슨 상관 계수"로 정의됩니다.
- 따라서 통계적 계산에서 순서척도(ordinal scale)가 적용되는 상관분석에서는 스피어먼 상관 계수가 사용되며 간격척도가 적용되는 변수들 간의 분석에서는 피어슨 상관 계수가 사용됩니다(위키피디아)
- 스피어만 상관계수의 식은 피어슨 상관계수와 동일합니다. 아래 그림의 왼쪽을 보시면 위에서 본 식과 동일한것을 볼 수있습니다. 다만, 스피어만 상관계수는 di = Xi - Yi 를 대입하여 오른쪽과 같이 변형하여 사용하는것이 일반적입니다.
(※ 스피어만 상관계수에서 1- 다음항 의 6은 다른 기호(시그마 등)가 아니라 숫자 6입니다!)
- 예를 들어, 한 고등학교 3학년 학생들의 모의고사 성적을 과목별로 등수를 매겼을 때, 언어영역 등수와 수리영역 등수간의 상관관계를 확인하기 위해서는 스피어만 상관계수로 분석할 수 있습니다.
- 빠른 이해를 위해 구체적으로 스피어만 점수를 구하는 예시를 보겠습니다.
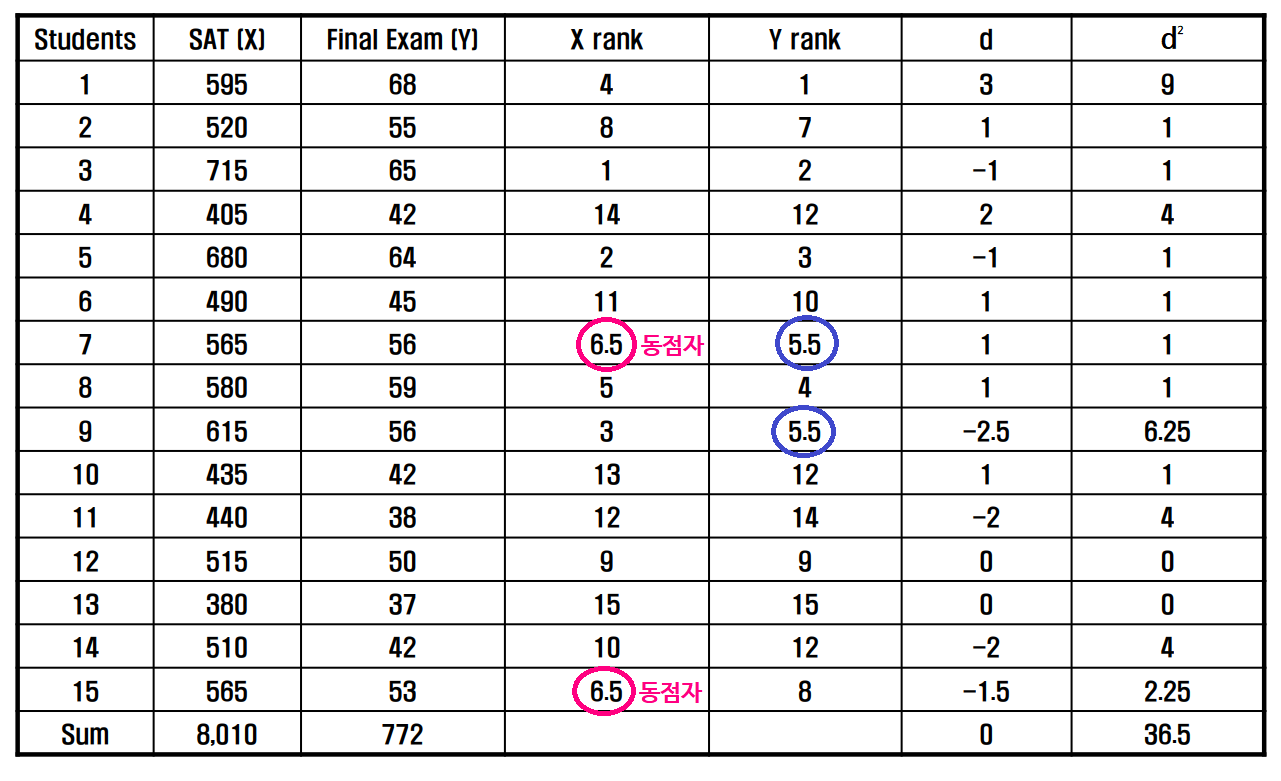
[예시] SAT 점수와 기말고사 성적이 순위척도로 되어있는 경우의 상관관계 분석
SAT 점수(X)의 순위와 기말고사 점수(Y)의 순위를 먼저 구합니다(X rank, Y rank). 여기서 주목할점은, 순위가 같은 경우에는 같은 점수를 부여합니다. 아래 X rank에서 SAT 점수가 565로 같은 2 데이터의 경우 6,7 위에 해당하는것을 6.5로 하여 동등하게 나누었습니다.
■ 공부할때 도움되시길 바라며, 두 상관계수(피어슨/스피어만)를 구하는 과정을 이해하기 쉽게 예제파일을 엑셀로 만들었습니다. 자유롭게 사용하셔도 되며, 사용시 댓글만 남겨주세요~
3. 상관관계의 해석
3.1 상관관계에 영향을 주는 요인들
1. 상관계수는 just 선형관계(linearity)
: 상관계수는 선형관계, 직선관계를 나타내는 값이기 때문에 직선이 아닌 형태의 관계를 가진 경우에는 나타낼 수가 없다는 한계점이 있기 때문에 꼭 상관계수를 볼때에는 산점도를 먼저 확인해야합니다.
: 아래 그림에서 0에 해당하는 핑크 박스의 경우들에도 모두 상관계수 값이 0이지만, 산점도를 보고 다른 경우의 수를 생각해서 추가적으로 분석할 수 있을 것입니다.

2. 관측치들이 충분한 변량을 가지고 있어야함
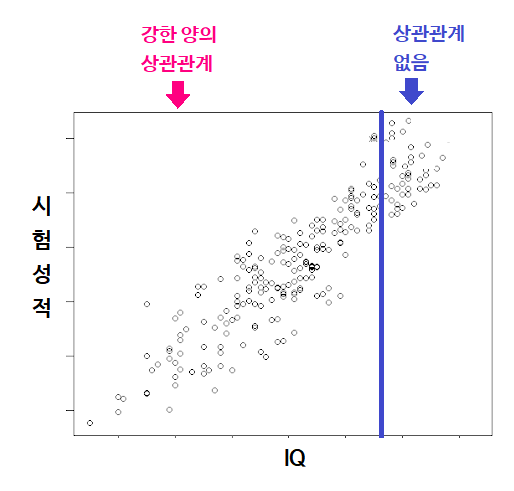
- 두 변수의 상관관계를 충분히 나타내기 위해서는 한 변수가 다른 변수에 대해서 충분한 변량을 가지고 있어야합니다.
- 예를 들어서 IQ와 시험성적간의 상관계수를 구한다고 할때, 확보한 IQ의 범위가 140 이상인 관측치밖에 없다면, 두 변수간 상관관계가 매우 낮게 나올 것입니다.
3. 관측수의 크기
- 일반적으로 상관관계를 계산하기 위한 샘플의 관측치 수는 상관관계의 크기에 영향을 주지 않습니다.
- 하지만 관측치 수의 크기가 커지면 상관관계의 정확도를 높일 수 있습니다.
3.2 상관관계의 해석
1. 상관계수의 스케일은?
- 상관계수는 순서형(ordinal) 척도입니다.
- 즉, 상관계수 r값이 0.4와 0.6간의 차이가 0.6과 0.8간의 차이와 동일하다고 할수 없으며, 0.4 값이 0.2의 2배에 해당된다고 말할수도 없습니다.
2. 상관계수 값의 해석
| 절대값 | 의미 |
| 0.9~1.0 | 매우 높은 음/양의 상관관계 |
| 0.7~0.9 | 높은 음/양의 상관관계 |
| 0.5~0.7 | moderate 음/양의 상관관계 |
| 0.0~0.1 | 상관관계가 거의 없음 |
3. '상관계수 0.2'의 의미는?
- 절대적인 숫자 값에 대한 해석은 연구자, 연구목적, 연구분여에 따라서 다를 수 있다. 즉, 의미있다고 볼 수도 있고 의미없다고 볼 수도 있습니다.
- 예를들어 암 치료에 효과적인 신약개발의 경우, 신약 투여량과 암의 회복속도 간의 상관관계가 0.2라고 할때, 일반적인 상황에서는 0.2가 낮은 약한 상관관계를 보인다고 할 수 있지만 의학계에서는 0.2라는 상관계수도 매우 중요한 발견이라고 여길 수 있습니다.
4. 상관계수와 유의수준(p-value)
- 상관계수와 p-value는 서로 다른 의미를 지닌 값입니다. 아래의 두 가지 경우를 예로 살펴보겠습니다.
1) 상관계수의 값은 크지만 p-value가 유의미하지 않은 경우
- 예를들어 r= 0.9 이지만 p=0.25인 경우, 높은 상관관계를 보이지만 p-value값이 터무늬없이 높습니다. 유의미하지 않은 값이죠. 즉 결과가 정확하다고 볼 수 없다는 의미입니다.
- 일반적으로 p값은 샘플의 크기에 영향을 받지만, 상관계수는 샘플의 크기와는 무관합니다. 이런 경우, 샘플의 수를 증가시켜보면 유의미한 p값을 얻을 수도 있습니다.
2) 상관계수의 값은 작지만 p-value가 유의미한 경우
- 예를들어 r= 0.035 이지만, p<0.05인 경우, 상관계수의 값은 작아서 두 변수의 상관관계는 없지만 p값은 아주 작아 유의미하다는 결론을 내릴 수 있습니다.
- 유의미 하다는것의 결론은 귀무가설을 기각한다는것이고, 이 경우에서는 H0 : 'r=0' 이라는 가설을 기각한다는 말입니다. 즉 상관관계 0.035의 값이 0이 아니라는 것을 의미합니다.
- 즉 r≠0 이지만, 그렇다고 r이 큰 값은 아니기 때문에 중요한 발견이라고 할 수는 없는 것이지요.
- 글의 상단에서 말씀드린것처럼 상관계수로는 두 변수의 인과관계를 알 수없고 단지 직선관계만 확인할 수 있다고 하였습니다. 그렇다면, 두 변수의 인과관계는 어떻게 확인할 수 있을까요? 그 방법이 바로 '회귀분석법'입니다. 다음 글에서는 회귀분석에 대해서 살펴보도록 하겠습니다.
2021.05.23 - [통계 분석(Statistics)] - [통계 기초] 선형회귀분석
[통계 기초] 선형회귀분석
hyen4110.tistory.com
'Statistics' 카테고리의 다른 글
| [통계] 선형회귀분석_회귀계수 추정과 T검정 (3) | 2021.06.13 |
|---|---|
| [통계] 선형회귀분석(Linear Regression) (2) | 2021.05.23 |
| [통계] 카이제곱 검정(Chi-squre test) (1) | 2021.04.27 |
| [통계] 05 두 집단 비교에 대한 추론 (0) | 2021.04.23 |
| [통계] 04 가설검정_1, 2종 오류와 유의수준 (0) | 2021.04.19 |




댓글