[딥러닝][기초] 활성화 함수(Activation Function)

Stanfoard CS231n 2017의 강의자료를 참고하여 작성하였습니다.

(www.youtube.com/watch?v=vT1JzLTH4G4&list=PL3FW7Lu3i5JvHM8ljYj-zLfQRF3EO8sYv&index=0)

1. 시그모이드 함수(Sigmoid)

수식	그래프	미분 그래프

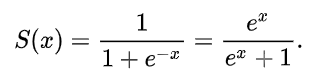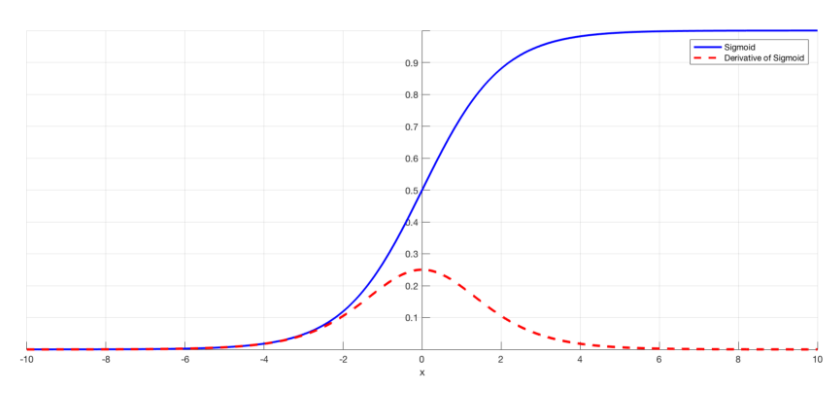[사진출처] 위키피디아/isaacchanghau.github.io/img/deeplearning/activationfunction/sigmoid.png

 

[특징]
1. 0에서 1사이의 값을 갖는다

   (squashes numbers to range [0,1])

   : 큰 값을 허락하지 않아서 gradient explosion을 방지하는데 좋았음(Good)

 

2. Vanishing Gradient 문제 발생 

: 시그모이드 함수의 양 극단에서 기울기가 0으로 수렴(Bad)

(Historically popular since they have nice interpretation as a saturating firing rate of a neuron)

 -> 기울기가 0에 가까워지면, 역전파 과정에서 전달이 되지 않으므로, 기울기 소실(Vanishing gradient) 문제가 발생

 -> 따라서 은닉층에서 시그모이드가 잘 사용되지 않음

 

  : "saturated"란?

   0으로 수렴해서 정보를 잃어버리는 것을 saturated라고 한다.

3. 0점 중심이 아님(not zero centered) (Bad)

: x가 0일때, 0.5의 값을 가진다. 

 (Sigmoid outputs are not zero-centered)

 -> 평균이 0 이 아니라 0.5이며 항상 output이 양수이기 때문에, 가중치는 

2. 쌍곡 탄젠트 함수(tanh, hyperbolic tangent)

수식	그래프	미분 그래프

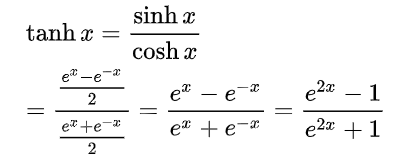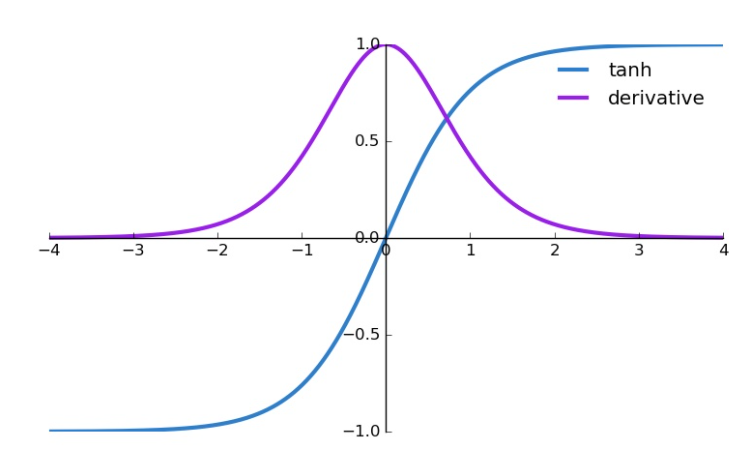[사진출처] 위키피디아/Ronny Restrepo

 

[특징]
1. -1에서 1사이 값을 갖는다

   (squashes numbers to range [-1,1])

 

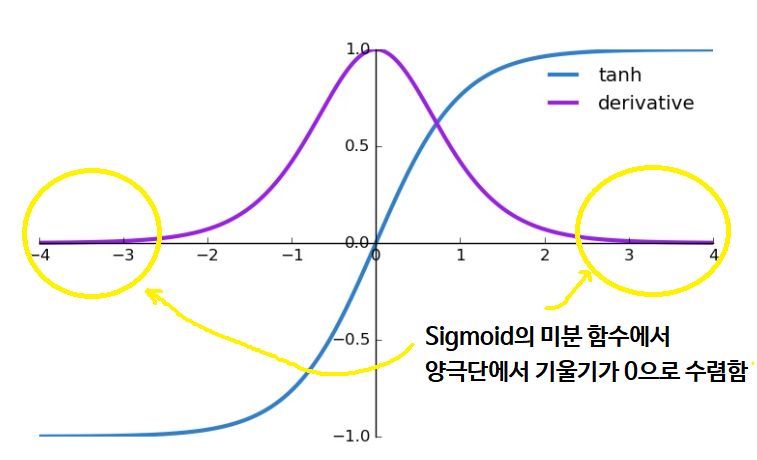
2. Vanishing Gradient 문제 발생 

: tanh 함수도 여전히 시그모이드 함수처럼 양 극단에서 기울기가 0으로 수렴 (Bad)

3. 영점 중심(zero-centered)

: 영점(0,0) 값을 지난다. (Good)

 

4. 0 중심에서 기울기(stiff)가 커서 값을 잘 보존한다 (Good)

 

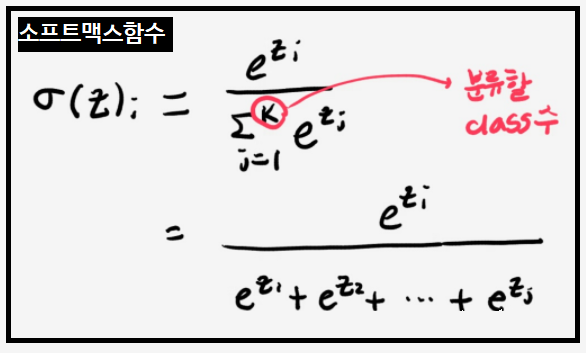
3. 소프트맥스 함수(Softmax function)

: k개의 값을 입력받아 합이 1이 되는 k개의 값을 출력하는 함수

: 입력값은 부호와 절대값의 제한이 없으나, 출력값은 0과 1사이로 출력되어 확률로 해석되기도 함.

: 입력값의 대소 관계는 출력값의 대소관계로 이어진다.

 

소프트맥스 함수의 출력과정 

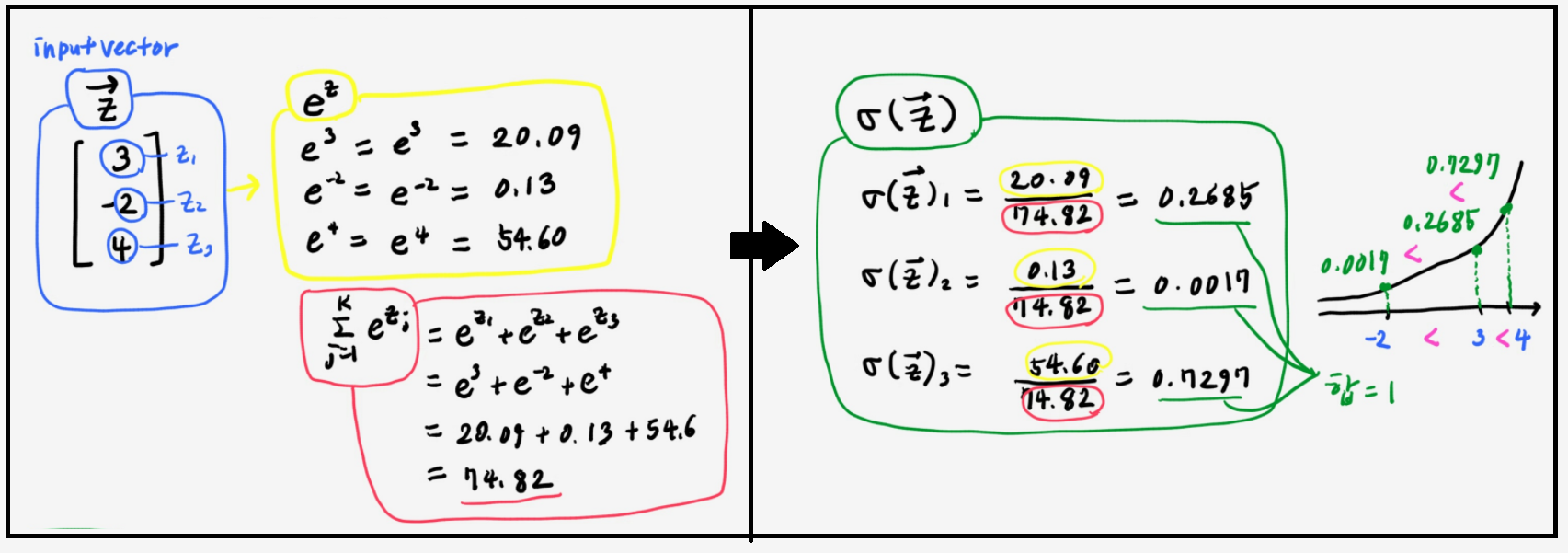
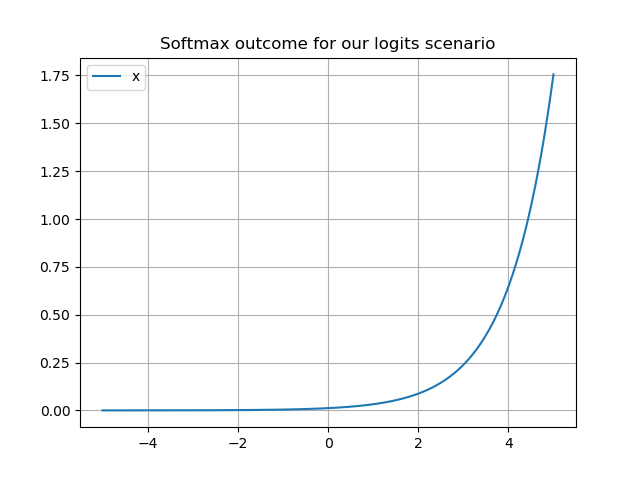
[특징]

1. 소프트맥스함수의 입력값에 정수를 더하더라도 출력은 변하지 않는다. Bad

 -> 이와같은 잉여성으로 인해 신경망 가중치 학습시, 가중치가 잘 수렴하지 않고 학습이 느리다는 단점이 있다

    이를 위해 대개의 경우 출력층에 몇가지 제약(regularization)을 추가한다

 

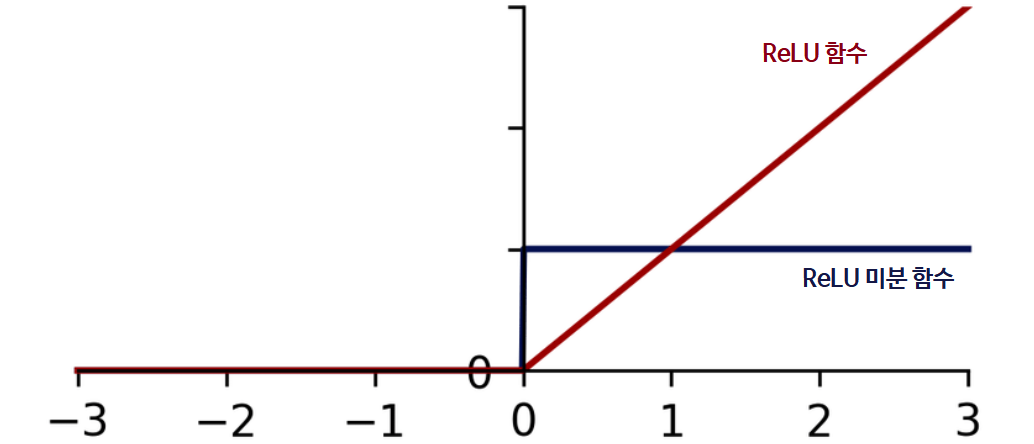
4. ReLU 함수

 

패밀리

1) ReLU 함수

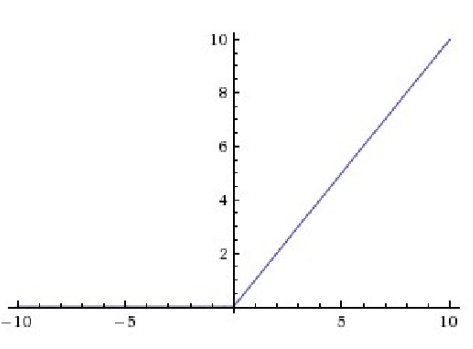
수식	그래프 f(x)	미분 그래프 f'(x)

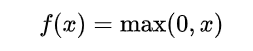[사진출처] 위키피디아/Research Gate

 

[특징]
1. Saturate 되지 않아서 어디서나 정보를 갖는다. (Good)

   (Does not saturate)

2. 컴퓨터 연산이 효율적이다.(Good)

3. 시그모이드, tanh 함수보다 수렴이 빠르다. (Good)

4. x가 음수일때 기울기가 모두 0 이 된다 (Bad)

5. 0에서 미분불가하다

   [Question] 미분이 불가해서 문제가 되지 않나요? 

   [Answer] 모든 실수 중에서 0을 선택할 확률은 0이다. 따라서 0에서 미분해야할 확률도 0이므로 걱정 No

               코딩 할때에는, x=0일때 미분이 되도록 하거나 smooth 하도록 코딩하면됨!

 

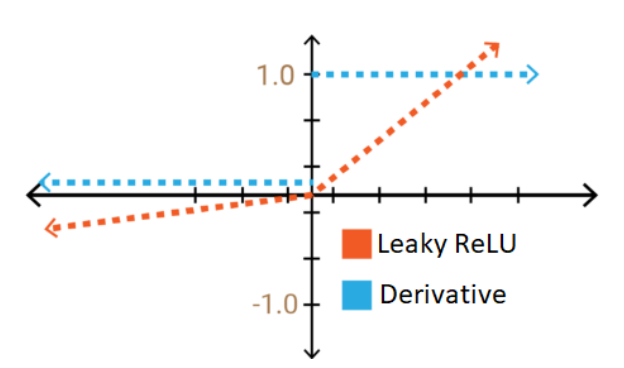
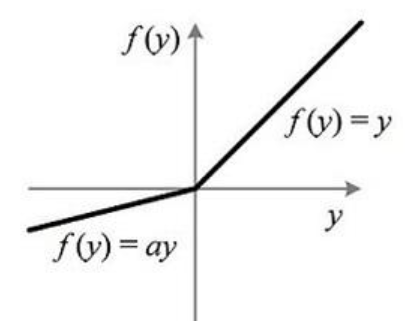
1) Leaky ReLU 함수

수식	그래프 f(x)	미분 그래프 f'(x)

[사진출처] 위키피디아/towards data science

 

[특징]

- ReLU 함수가 가진 장점을 모두 갖고 있다. (Good)

<ReLU 패밀리 장점> 1. Saturate 되지 않아서 어디서나 정보를 갖는다. (Good) 2. 컴퓨터 연산이 효율적이다.(Good) 3. 시그모이드, tanh 함수보다 수렴이 빠르다. (Good)

- x가 음수일때에도 기울기가 0 이 아닌 0.1로 정보가 손실되지 않는다. (Good)

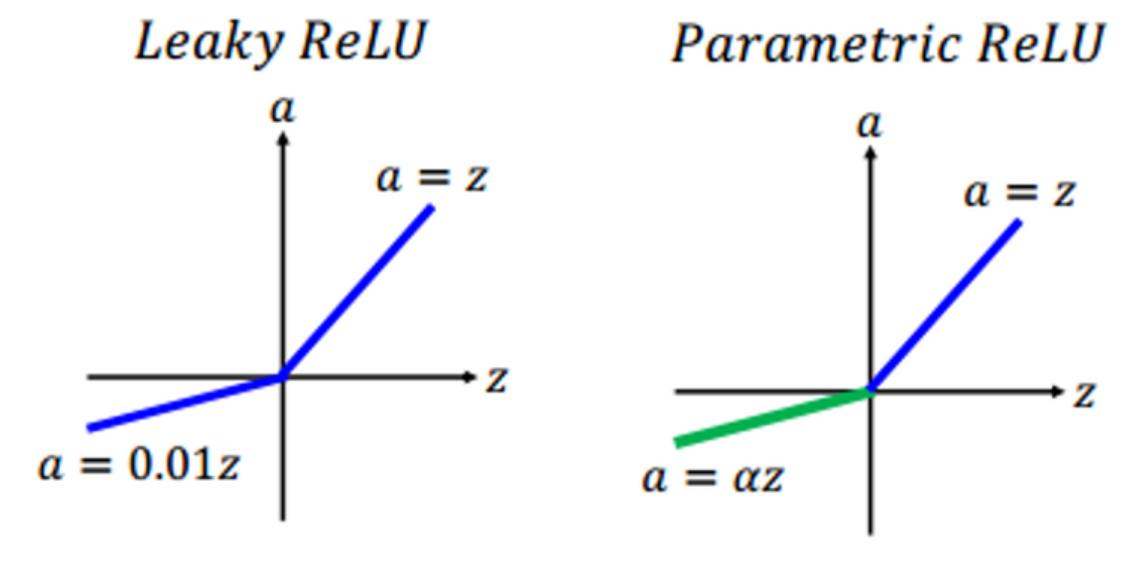
2) PReLU(Parametric Rectifier)

수식	그래프 f(x)	미분 그래프 f'(x)

[사진출처] 위키피디아/programmersought

 

[특징]

- ReLU 함수가 가진 장점을 모두 갖고 있다. (Good)

<ReLU 패밀리 장점> 1. Saturate 되지 않아서 어디서나 정보를 갖는다. (Good) 2. 컴퓨터 연산이 효율적이다.(Good) 3. 시그모이드, tanh 함수보다 수렴이 빠르다. (Good)

- Leaky ReLU의 일반화 버전

- 음수일때의 기울기 alpha는 학습할 수 있도록 파라미터로 설정되어 있음.

 

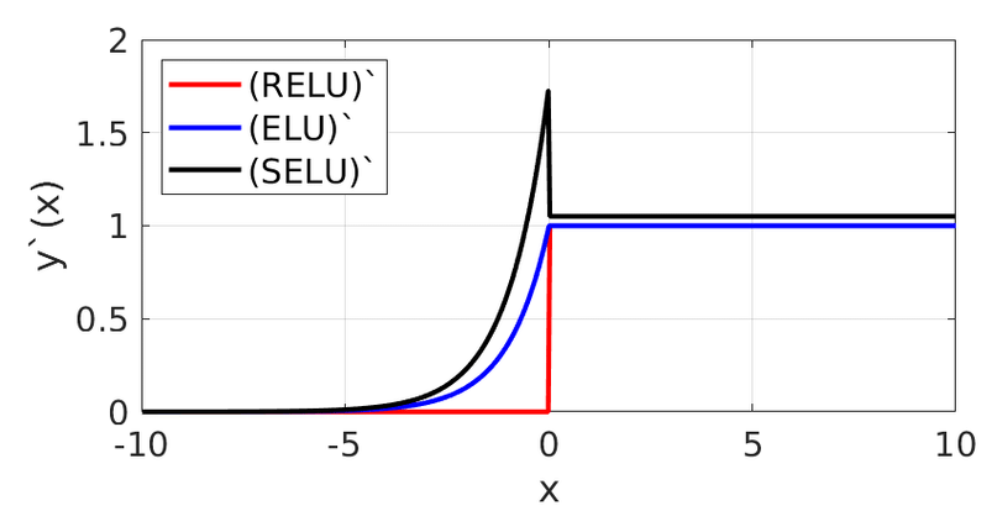
3) ELU(Exponential Linear Units)

수식	그래프	미분 그래프

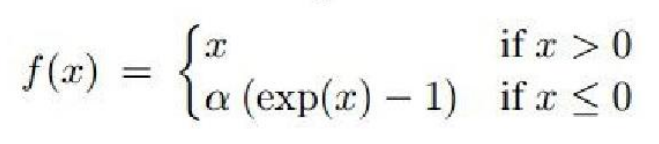[사진출처] 위키피디아/researchgate

 

[특징]

- ReLU 함수가 가진 장점을 일부 갖고 있다. (Good)

<ReLU 패밀리 장점> 1. Saturate 되지 않아서 어디서나 정보를 갖는다. (Good) 2. 컴퓨터 연산이 효율적이다.(Good) 3. 시그모이드, tanh 함수보다 수렴이 빠르다. (Good)

- x가 음수일때에도 기울기가 0 이 아닌 0.1로 정보가 손실되지 않는다. (Good)

- zero mean에 가까운 출력을 보인다. (Good)

  (Closer to zero mean outputs)

- exponential 함수 exp()에 대한 연산비용 필요. (Bad)