2021.05.23 - [통계 분석(Statistics)] - [통계 기초] 상관관계(Correlation Coefficient)
[통계 기초] 상관관계(Correlation Coefficient)
1. 상관관계(Correlation Coefficient) 1.1 상관관계란? - [의미] 상관관계는 두 변수 간의 직선관계를 나타냅니다. 상관관계가 있다는 것은 인과관계가 있다는것이 아닙니다. 상관관계가 높다고해서 두
hyen4110.tistory.com
이전 글에서는 상관관계 분석에 대해서 알아보았습니다. 상관관계는 두 변수간의 상관관계는 알 수 있었지만 두 변수가 서로 간에 영향을 주는지에 대해 확인할 수 없었습니다. 하지만 회귀분석에서는 변수가 서로 영향을 주는지, 즉 인과관계를 확인할 수 있는 분석방법입니다.
1. 선형회귀분석이란?
- 두 변수 간의 관계가 존재하는가 여부는 상관분석으로 확인할 수 있지만, 회귀분석은 그 변수들 간에 존재하는 관계를 정확하게 나타낼 수 있는 수학식 또는 모형을 개발해서 인과관계를 파악하는 것이 목적입니다.
- 회귀분석은 다른 변수(독립변수)들에 기초해서 한 변수의 값(종속변수)의 값을 예측하기 위하여 사용합니다.
| Y변수 | X변수 |
| : 독립변수들에 영향을 받아서 변화하는 변수 : 종속적인/의존적인 변수 : 연구자가 알고싶어하는 변수 : 1개만 존재 : [동의어] 결과, 반응변수, 목표변수, 종속변수 |
: 다른 변수들에 의해서 영향을 받지 않음 : 연구자가 마음대로 조정할 수 있는 변수 : 1개 이상 존재 : [동의어] 원인, 설명변수, 예측변수, 독립변수 |
1.1 회귀분석의 기본 가정
: "독립변수 X가 종속변수 Y에 영향을 준다" ( <-> 'Y가 X에 영향을 준다' or 'X와 Y는 무관하다')
1.2 회귀분석의 목적
- 점과 선 사이의 오차(제곱합)을 최소로하는 직선을 찾는것(최소제곱법 또는 최소자승법)
- 오차제곱합(SSE, Sum of Squared prediction error)
: 추정된 선으로부터 점들이 얼마나 떨어져있는가에 대한 정도
*SSE = Σ(Yi-Yi')²

* RMSE, Root Mean Squre Error)

: 추정된 선으로부터 점들이 평균적으로 얼마나 떨어져 있는가의 정도
| [Question] 왜 n-2일까? n-1(df)도 아니고? -> 선형회귀식에서 a와 b값이 고정되어 있으므로 2를 빼준다 => 따라서, 만약 독립변수가 1개가 아니라 3개라면 n-2가 아닌 n-4이 된다 |
- 결론적으로 선형회귀분석의 목적은, 오차제곱합(추정된 선으로부터 점들이 떨어진 정도)를 최소화하는 회귀계수(parameter) a, b를 찾는 것 입니다. 이때 최소화해야하는 오차제곱합을 머신러닝에서는 비용함수(cost function)라고도 합니다.
- 선형회귀모델에서의 비용함수는 convex 형태, 즉 global(전역) 최적해가 존재하는 형태이기 때문에, a와 b에 대하여 각각 비용함수를 편미분한뒤 0이 되는 값을 구합니다. 식이 2개, 미지수가 2개로 답이 하나가 나오며 그 답은 아래와 같습니다.
2. 단순 회귀모형

1. 회귀계수(Regression Coefficient)
- 회귀식의 기울기(b)와 절편(a)는 회귀모형의 회귀계수이다.
| 회귀계수 | 설명 |
| b (기울기) | - 기울기는 b는 방향성을 의미하 데이터 측정단위에 의존 * 회귀계수 b 구하는 식  ※ 회귀선 기울기값을 강도와 상관이 없다. : 기울기만큼 X에 따라 Y가 변하는데 어떻게 강도와 상관이 없다는걸까요? : 그 이유는 회귀선 기울기(b)는 얼마든지 측정 단위에 따라 달라질 수 있다는 점에 있습니다. 예를 들어 측정단위를 어떻게 했느냐에 따라 b는 0.23이 2.3이 될수도 있지만, 측정단위만 변경했기 때문에 사실상 강도는 같은 것입니다! - 회귀선 기울기의 해석 : X가 1 증가할때마다 Y가 회귀선 기울기 만큼 증가한다. |
| a (절편) | a = E(Y)-b1*E(X) |
3. 회귀모형의 타당성
3.1 Case 1,2 가정
- 회귀모형의 타당성은 두가지 상황을 가정하고 진행합니다. 하나는 X에 대한 정보가 없어 Y의 평균으로 예측을 하는 상황(Case1)과 X에 대한 정보를 가지고 Y를 예측하는 상황(Case2) 입니다.
- 두 상황을 비교하여 추정값이 평균값에 비하여 얼마나 잘 설명을 하는지를 계산하고자 합니다.
- 만약 X와 Y 변수가 강력한 선형관계(상관관계)가 있다면, 추정식으로부터 추정되 값 ŷ 이 ȳ 보다 더 좋은 추정치가 될 것입니다.
| Case#1 X에 대한 정보 없이 Y 예측 |
- Y에 대한 가장 좋은 추정값 = ȳ (Y의 평균) - 추정 에러(prediction error) = y-ȳ - 총 추정 에러(total prediction error, E1) = Σ(y-ȳ)² = TSS(total sum of squres) -> (※TSS를 SST라고 표기하기도함!) |
| Case#2 X에 대한 정보를 가지고 Y 예측 |
- Y에 대한 가장 좋은 추정값 = ŷ = a+bx - 추정 에러(prediction error) = y-ŷ - 총 추정 에러(total prediction error, E2) = Σ(y-ŷ)² = SSE(the sum of squred error) |
3.2 모형의 적합도 판단(goodness-of-fit-test)
- 반응변수 Y의 총 변동량을 2개로 분해하여 첫째는 회귀식에 의한 변동, 즉 X에 의해서 설명되 변동과 둘째는 그외 나머지 잔차에 의하여 설명된 변동으로 모형의 적합도를 판단합니다.
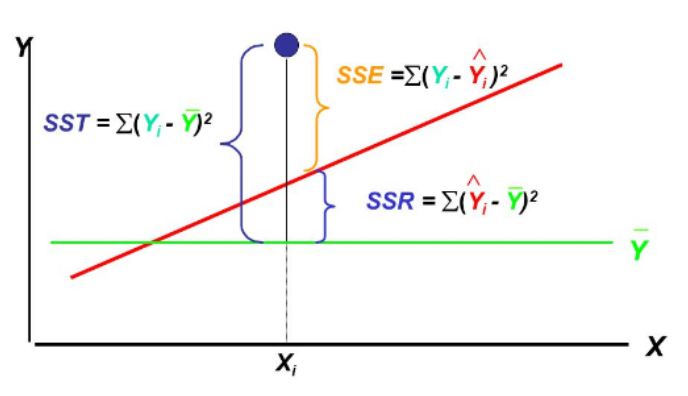
| SST (total sum of squares) |
ȳ 대비 Y의 총 변동 = Y의 총 변동량 |
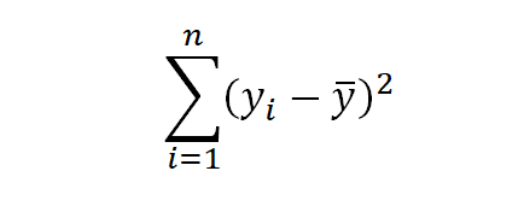 |
| SSR (regression sum of squares) |
SST 중에서 ŷ이 Y를 설명하는 변동 = X변수에 의해서 설명된 양 |
 |
| SSE (error sum of squares) |
SST 중에서 ŷ이 Y를 설명하지 못하는 변동 = 에러에 의해서 설명된 양 |
 |
3.3 결정계수(R2)
: Y의 총 변동량 중에서 X에 의해서 설명된 분량으로 '표본에 대한 회귀모형의 설명력'을 의미하며, 값이 클수록(1에 가까울수록) 모형이 적합하다고 평가할수 있습니다.
= '단순히 Y의 평균값을 사용했을 때 대비 X 정보를 사용함으로써 얻는 성능 향상 정도'
= 'X변수가 Y변수의 분산을 얼마나 줄였는가에 대한 정도
(https://www.youtube.com/watch?v=ClKeKeNz7RM)
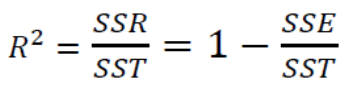
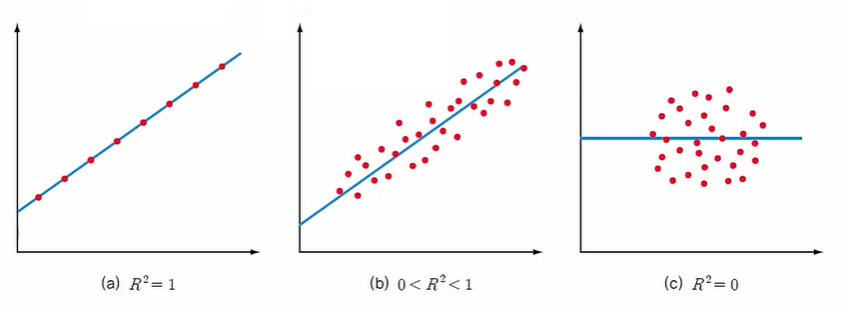
- R2값의 의미
| R2 = 1 | - 추정된 회귀직선(회귀모형)으로 Y의 총 변동이 완전히 설명된다. - 모든 측정값들이 회귀직선에 있는 경우. |
| R2 = 0 | - 추정된 회귀직선(회귀모형)은 X와 Y의 관계를 전혀 설명하지 못한다. |
3.4 수정 결정계수 (Adjusted R2)
- R2의 한계점
: R2는 유의하지 않은 변수가 추가되더라도 항상 증가하는 경향이 있다. 전혀 상관없는 변수라도, 상관관계가 아주 조금은 있기 때문이다. 0.0이 나올 수는 없기 때문입니다.
: 따라서 수정 R2는 특정 계수를 곱함으로써 값을 보정하여, 유의하지 않은 변수가 추가될 경우 증가하지 않도록 하는 역할을 합니다.

3.5 결정계수(R2)와 p-value
| 낮은 R2 & 낮은 p-value (p-value<0.05) | 모델의 설명력이 낮지만, 모델이 유의미함(better than not having a model) |
| 낮은 R2 & 높은 p-value (p-value>0.05) | 설명력이 낮고, 모델이 유의미하지 않음(worst scenario) |
| 높은 R2 & 낮은 p-value (p-value<0.05) | 모델 설명력이 높고, 모델이 유의미함(best scenario) |
| 높은 R2 & 높은 p-value (p-value>0.05) | 모델 설명력이 높지만, 모델이 유의미하지 않음(worthless) |
*공부에 도움이 되시길 바라며, 선형회귀계수와 결정계수(R2)값을 구하는 과정을 엑셀파일 예제로 첨부하였습니다. 자유롭게 사용하시고 댓글만 남겨주세요 :)
이번글에서는 회귀계수를 구하고, 그 회귀계수가 얼마나 설명력이 있는지(표본 측정치를 얼마나 잘 설명하는지) 확인하는 적합도 검정을 해보았습니다. 다음 글에서는 단순선형회귀분석의 유의성 검정을 어떻게 할 수있는지에 대하여 살펴보겠습니다.
2021.06.13 - [통계 분석(Statistics)] - [통계]단순선형회귀분석의 유의성 검정
[통계]단순선형회귀분석의 유의성 검정
지난 글에서는 선형회귀분석에 대해서 살펴보면서, 회귀식은 어떻게 추정하는지 그리고 그렇게 추정된 회귀모형이 얼마나 설명력이 있는지 결정계수 R2를 가지고 적합도를 판단할 수있음을 보
hyen4110.tistory.com
'Statistics' 카테고리의 다른 글
| [통계] 선형회귀분석_결정계수와 F검정 (6) | 2021.06.13 |
|---|---|
| [통계] 선형회귀분석_회귀계수 추정과 T검정 (3) | 2021.06.13 |
| [통계] 상관관계(Correlation Coefficient) (6) | 2021.05.23 |
| [통계] 카이제곱 검정(Chi-squre test) (1) | 2021.04.27 |
| [통계] 05 두 집단 비교에 대한 추론 (0) | 2021.04.23 |




댓글