이 글에서는 김성범 교수님의 강의자료를 일부 참고하였습니다. 공부를 하면서 찾아본 강의 중 가장 흐름이 이해가 잘되고 자료가 깔끔하여서 강력히 추천드립니다! :D
https://www.youtube.com/watch?v=ClKeKeNz7RM
지난 선형회귀분석 설명에서 결정계수 R2에 대해서 간단히 살펴보았습니다.
2021.05.23 - [통계 분석(Statistics)] - [통계] 선형회귀분석(Linear Regression)
[통계 기초] 선형회귀분석(Linear Regression)
2021.05.23 - [통계 분석(Statistics)] - [통계 기초] 상관관계(Correlation Coefficient) [통계 기초] 상관관계(Correlation Coefficient) 1. 상관관계(Correlation Coefficient) 1.1 상관관계란? - [의미] 상관..
hyen4110.tistory.com
위의 글과 같은 내용을 보시기 편하게 아래 다시 붙여넣도록 하겠습니다.
1. 결정계수(R2)
1.1 결정계수(R2)란? [복습]
: Y의 총 변동량 중에서 X에 의해서 설명된 분량으로 '표본에 대한 회귀모형의 설명력'을 의미하며, 값이 클수록(1에 가까울수록) 모형이 적합하다고 평가할수 있습니다.


| SST (total sum of squares) |
ȳ 대비 Y의 총 변동 |  |
| SSR (regression sum of squares) |
SST 중에서 ŷ이 Y를 설명하는 변동 |  |
| SSE (error sum of squares) |
SST 중에서 ŷ이 Y를 설명하지 못하는 변동 |  |
1.1 결정계수(R2)와 분산
- 결정계수(R2)와 분산은 무슨 상관이 있을까요? 왜 글의 제목은 결정계수와 분산분석일까요?
- 결정계수(R2)를 구할때 쓰는 SST, SSR,SSE는 모두 '차이의 제곱의 합'으로 일종의 분산이라고 할 수 있습니다.
- 결정계수(R2)도 'Y의 총 변동량 중에서 X에 의해서 설명된 분량' 이라고 하였는데요, 다른 말로는 'X변수가 Y변수의 분산을 얼마나 줄였는가에 대한 정도' 로 할수 있습니다.
: 예를 들어 R2값이 1이라면, Y분산을 100% 줄인것이고, 0.2라면 20% 줄였다고 말할 수있습니다)
2. 분산분석(ANOVA/Analysis of Variance)
2.1 귀무가설과 대립가설
| 귀무가설(H0) | b(b1, b2, ....bn) =0 = "모든 회귀계수는 0이다" |
| 대립가설(H1) | b(b1, b2, ....bn) ≠ 0 = "모든 회귀계수의 기울기는 0이 아니다" = "하나라도 0이 아닌값이 존재한다." |
2.2 검정통계량

- SSR은 X변수에 의해서 설명된양, SSE는 에러에 의해서 설명된 양입니다. 즉 SSR/SSE의 비율을 비교한다는것은 Y가 X변수에 의해서 더 설명이되는지, 에러에의해서 더 설명이 되는지 비교하고자 함임을 알 수 있습니다.
- 하지만 SSR/SSE가 얼마나 커야 큰 값으로 인정할수 있을까요?
-> 얼마나 커야 인정할 수 있는지에 대한 답은 늘, 우리는 분포에서 찾았습니다.
- 그렇다면, SSR/SSE의 분포는 어떻게 구하나요?
-> 아쉽게도 SSR/SSE에 대한 분포는 직접적으로 구할수가 없습니다.
그러나 SSR과 SSE는 각 카이제곱 분포를 따르는것을 알고있습니다(∵분산은 카이제곱분포를 따르기 때문)
<카이제곱 분포란?> |
- SSR/SSE의 분포를 알고싶은거지 SSR, SSE 각각이 카이제곱 분포를 따르는게 왜 중요할까요?
-> F분포의 정의에 따르면, 카이제곱분포를 따르는 두 변수를 나누면 F분포를 따른다는것을 알수있습니다.
=> 즉 SSR/SSE가 얼마나 큰지는 해당되는 F분포를 찾아서 확인할 수 있습니다.
<F분포란?> |
- SSR과 SSE가 따르는 카이제곱분포, 그리고 SSR/SSE가 따르는 F분포를 정리해보면 아래와 같습니다.

<ANOVA TABLE>
- 위에서 설명한것을 정리하면 아래와 같습니다. 아래는 실제 분산분석 결과 table과 같은 구조입니다.
| Source | SS | df(자유도) | MS | F | P |
| Model Error |
SSR | 1 | MSR = SSR/1 | F* = MSR/MSE ~F(1,n-2) |
|
| SSE | n-2 | MSE = SSE/(n-2) | |||
| Total | SST | n-1 | Sy² = SST/(n-1) |
- 여기서 왜 SS값이 있는데 자유도(df)로 나누어주어서 MS값을 구할까요?
-> F분포를 구할때, 각각의 자유도로 나눈 값을 분자분모로 취해주어야하기 때문에 그렇습니다!
- 회귀계수에 대한 t검정 결과 table에서 각 회귀계수 별로 p-value가 존재했던 것과 달리, F검정에서는 모든 회귀계수에 대해서 한꺼번에 검정하기 때문에 단 하나의 p-value가 나옵니다.
- 그렇기 때문에 단순선형회귀에서는 t검정의 귀무가설이나 f검정의 귀무가설이나 모두 하나의 기울기 b1=0이 되는것이 귀무가설이기 때문에 검정 결과가 같습니다.
| t검정 | F검정(분산분석) | |
| 귀무가설 | b1 = 0 ("기울기 b1은 0이다") | b(b1, b2, ....bn) =0 ("모든 회귀계수는 0이다") |
| 검정통계량 |  |
 |
| 결과(단순회귀) |  |
 |
| 결과(다중회귀) | 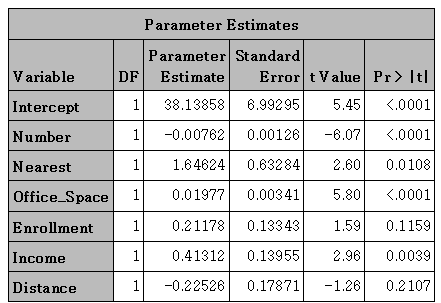 |
 |
✅ [질문] 다중회귀분석에서 f검정없이 t검정만으로도 가능하지 않을까요?
👉 No, ∵ t검정의 1종오류
일반적으로 사용하는 0.05의 유의수준으로 검정을 했을때,
5%라는 1종 오류가 발생할 가능성이 있다고 할 수 있습니다.
100개의 변수가 있을 때 5개에 대해서는
사실 기울기 b(j)=0이지만, b(j)≠0 이라고 결론을 낼 수 있습니다!
따라서, 다중회귀분석에서는 먼저 F검정을 통해
'모든 회귀계수가 0은 아니다'(=일부는 유의미하다) 것을 확인한 뒤에
개별 회귀계수에 대한 t검정을 실시하여 선형 관계를 밝혀내는 것이 일반적입니다.

아래는 위의 다중회귀 결과표에 등장하는 데이터에 대한 추가 설명 자료입니다


'Statistics' 카테고리의 다른 글
| [통계] 분산분석(ANOVA) (0) | 2021.06.13 |
|---|---|
| [통계] 다중선형회귀(Multivariable Linear Regression) (0) | 2021.06.13 |
| [통계] 선형회귀분석_회귀계수 추정과 T검정 (3) | 2021.06.13 |
| [통계] 선형회귀분석(Linear Regression) (2) | 2021.05.23 |
| [통계] 상관관계(Correlation Coefficient) (6) | 2021.05.23 |




댓글